A equação de segundo grau pode ser representada como:
Sendo que Δ (delta) dada por:
Se Δ>0 então raízes serão dadas por:
=
Lembre-se que as raízes representam os valores de x para os quais, y assume valor zero. Graficamente, isto corresponde aos pontos onde a curva corta o eixo X.
Para traçarmos o gráfico desta função, basta considerar A, B e C como dados de entrada e a saída da pela equação da função. De forma que para cada novo valor de x é calculado um valor de y(x), usando os mesmos valores de A, B e C:
Abaixo temos como ficou o gráfico no Excel, baseado nesta idéia:
 |
| Figura 1- Gráficoda Função do Segundo Grau |
Para fazer este gráfico, siga os seguintes passos:
- Abra o Excel
- Na célula A1 digite A. Na célula A2, digite B e na célula A3 digite C.
- Nas células B1, B2 e B3 digite os valores 3, 5 e -50
- Nas células D1,D2 e D3 digite respectivamente delta, r1 e r2.
- Na célula E1, insira a fórmula do cálculo do delta como: =B2^2-4*B1*B3
- Na célula E2, insira a fórmula do cálculo da raiz r1 como :=(-B2-RAIZ(E1))/(2*B1). Note como é a notação para extrair raiz quadrada, basta usar o termo raiz(E1 )
- Na célula E3, insira a fórmula do cálculo da raiz r2 como: =(-B2+RAIZ(E1))/(2*B1)
- Na célula A7, digite x
- Na célula B7, digite y(x)
- Nas células A8 até A23, digite respectivamente os valores de -8 até 7.
- Na célula B8, insira a fórmula como: =$B$1*A8^2+$B$2*A8+$B$3. Note que novamente usamos os símbolos de $ para fixar linha e coluna.
- Copie a fórmula digitada em B8 e cole de B9 até B23
- Agora selecione as duas colunas de dados de A7 até A23 e B7 até B23 ao mesmo tempo.
- Em seguida, selecione a aba Inserir e escolha gráfico do tipo dispersão com Linhas Suaves.
- E voilá, o seu gráfico ficará pronto.
 |
| Figura 2 - Gráfico de Dispesrão com Linha Suaves |
A | -1 | 1 | -1 | -2 |
C | 25 | 10 | 6 | 2 |
b | 5 | 2 | 3 | -12 |
Note que com os valores -2,2 e -12 não temos raízes, mas temos o gráfico.Note que o gráfico nunca corta o eixo X.
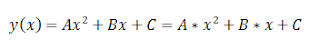


Nenhum comentário:
Postar um comentário